Establish timing budgets for nets

• Gate and wire delays must be optimized during timing driven layout design
• Wire delays depend on wire lengths
• Wire lengths are not known until after placement and routing

Delay budgeting with the zero slack algorithm

• Let vi be the logic gates and ei be the nets
• Let DELAY(v) and DELAY(e) be the delay of the gate and net, respectively
• Timing budget TB(v) of a gate corresponds to DELAY(v) + DELAY(e)

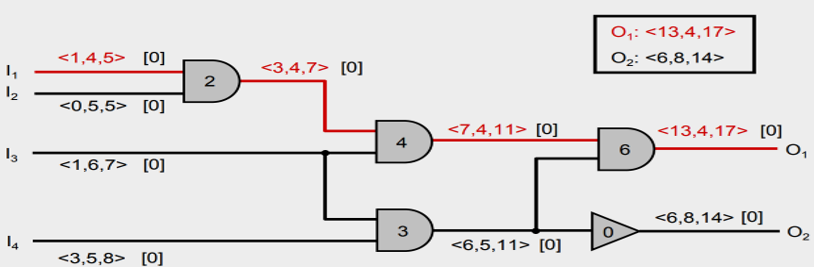
Example: Use the zero slack algorithm to distribute slack

• Format: <AAT, Slack, RAT>, [timing budget]
• Find the path with the minimum slack

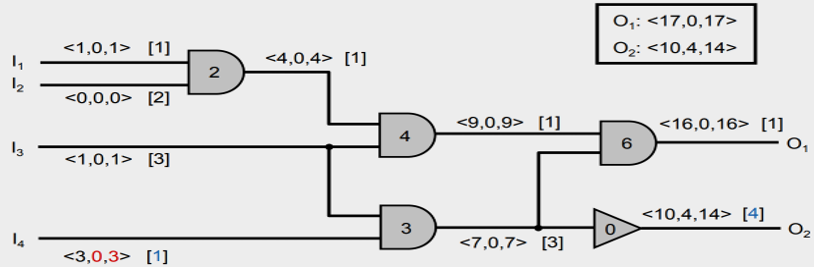
• Distribute the slacks and update the timing budgets

• Before the application of the algorithm
• After the application of the algorithm

Forward path search

• Forward Path Search (FORWARD_PATH(vmin,G))
• Input: node vmin with minimum slack slackmin, timing graph G
• Output: maximal downstream path path from vmin such that no node v ∈ V affects the slack of path

  1. path = vmin
  2. do
  3.  flag = false
  4.  node = LAST_ELEMENT(path)
  5.  foreach (fanout node fo of node)
  6.      if ((RAT[fo] == RAT[node] + TB[fo]) and (AAT[fo] == AAT[node] + TB[fo]))
  7.          ADD_TO_BACK(path,fo)
  8.          flag = true
  9.          break
  10. while (flag == true)
  11. REMOVE_FIRST_ELEMENT(path) // remove vmin
  

Backward path search

• Backward Path Search (BACKWARD_PATH(vmin,G))
• Input: node vmin with minimum slack slackmin, timing graph G
• Output: maximal upstream path path from vmin such that no node v ∈ V affects the slack of path

  1. path = vmin
  2. do
  3.  flag = false
  4.  node = FIRST_ELEMENT(path)
  5.  foreach (fanin node fi of node)
  6.      if ((RAT[fi] == RAT[node] –TB[fi]) and (AAT[fi] == AAT[node] –TB[fi]))
  7.          ADD_TO_FRONT(path,fi)
  8.          flag = true
  9.          break
  10. while (flag == true)
  11. REMOVE_LAST_ELEMENT(path) // remove vmin
  

Delay Budgeting With the Zero Slack Algorithm

• Input: timing graph G(V,E)
• Output: timing budgets TB for each v ∈ V

  1. do
  2.  (AAT,RAT,slack) = STA(G)
  3.  foreach (vi ∈V)
  4.      TB[vi] = DELAY(vi) + DELAY(ei)
  5.  slackmin = ∞
  6.  foreach (v ∈ V)
  7.      if ((slack[v] < slackmin) and (slack[v] > 0))
  8.          slackmin = slack[v]
  9.          vmin = v
  10. if (slackmin ≠ ∞)
  11.     path = vmin
  12.     ADD_TO_FRONT(path,BACKWARD_PATH(vmin,G))
  13.     ADD_TO_BACK(path,FORWARD_PATH(vmin,G))
  14.     s = slackmin / |path|
  15.     for (i = 1 to |path|)
  16.         node = path[i] // evenly distribute
  17.         TB[node] = TB[node] + s // slack along path
  18. while (slackmin ≠ ∞)